반응형
개요
이번에는 최단 경로를 구하는 방법 중 하나인
디엑스트라를 이용하여 문제를 풀어 보도록 하겠습니다.
문제

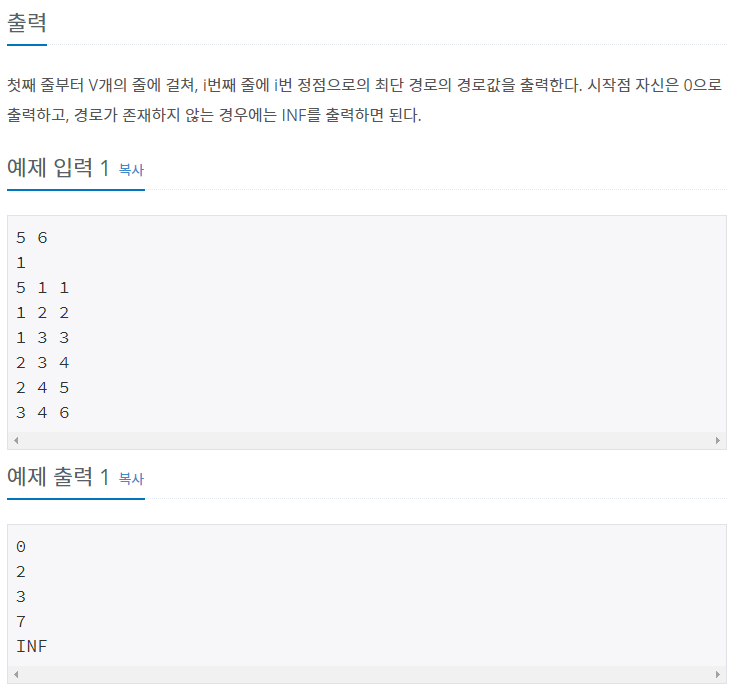
풀이
다익스트라 알고리즘은 시작점을 기준으로 인접한 노드들을 방문하여 시작점에서의
최소거리를 찾는 알고리즘으로 인접한 노드들을 방문한 뒤에는 인접한 노드들의
인접한 노드들의 거리를 찾아 비교해 가며 최단 거리를 설정하는 알고리즘입니다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int MAX = 20000 + 1;
const int INF = 987654321;
int V, E, K;
vector<pair<int, int>> graph[MAX];
vector<int> dijkstra(int start, int vertex)
{
vector<int> distance(vertex, INF); //start를 기준으로 거리
distance[start] = 0; //자기 자신한테 가는 비용 0
priority_queue<pair<int, int>> pq; //Cost, Vertex
pq.push(make_pair(0, start)); //초기 비용과 시작점
while (!pq.empty())
{
int cost = -pq.top().first; //거리의 부호를 바꾸어 거리가 작은 정점부터 꺼내지게 하였으므로 부호를 바꿔준다
int curVertex = pq.top().second;
pq.pop();
//최소거리를 원하므로
if (distance[curVertex] < cost)
continue;
//neighbor 다 확인
for (int i = 0; i < graph[curVertex].size(); i++)
{
int neighbor = graph[curVertex][i].first;
int neighborDistance = cost + graph[curVertex][i].second;
//최소 경로 발견시 업데이트
if (distance[neighbor] > neighborDistance)
{
distance[neighbor] = neighborDistance;
//거리의 부호를 바꾸어 거리가 작은 정점부터 꺼내지도록하기 위해
pq.push(make_pair(-neighborDistance, neighbor));
}
}
}
return distance;
}
int main(void)
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> V >> E >> K;
V++; //정점번호 1부터 시작
for (int i = 0; i < E; i++)
{
int source, destination, cost;
cin >> source >> destination >> cost;
graph[source].push_back(make_pair(destination, cost));
}
vector<int> result = dijkstra(K, V);
for (int i = 1; i < V; i++)
{
if (result[i] == INF)
cout << "INF\n";
else
cout << result[i] << "\n";
}
return 0;
}
반응형
'알고리즘 & 자료구조 > 알고리즘 (백준문제)' 카테고리의 다른 글
| 알고리즘 - 최대공약수 구하기 (유클리드 호제법) - C++ (0) | 2020.05.10 |
|---|---|
| 백준 Back_Joon(11650 좌표정렬)- C++ (0) | 2020.05.01 |
| 백준 Back_Joon (11047 동전0 문제) - C++ (0) | 2020.05.01 |
| 백준 Back_Joon (14697 방 배정하기) -C++ (0) | 2020.04.28 |